3. Optimisation pour l’exploration humaine
Dans la partie précédente, nous avons détaillé les différents paramètres physiques et biologiques qui doivent être pris en compte d’un point de vue théorique pour faire de l’imagerie avec des traceurs émetteurs de positons. Avant d’étudier plus en détail les points particuliers pour l’exploration expérimentale de modèles animaux, nous allons préciser les caractéristiques spécifiques de la caméra TEDC utilisée en routine pour l’exploration des patients en oncologie. Nous détaillerons les différents paramètres à optimiser dans les acquisitions et dans le traitement des données à partir d’acquisitions réalisées sur fantôme.
3.1 Principe de fonctionnement d’une caméra TEDC (Picker Axis)
3.1.1 Généralités
En tomographie d’émission de positon, l’enregistrement d’un événement correspond à la détection en coïncidence des photons d’annihilation issus de la désintégration β+. Le circuit de coïncidence qui relie les deux détecteurs placés à 180° n’autorise l’enregistrement d’un événement que si les deux photons sont détectés au cours d’un intervalle de temps ou fenêtre de coïncidence de 15 ns. Chaque coïncidence permettra ainsi de définir la direction des deux photons d’annihilation faisant suite à l’émission du β+. Chaque projection sera construite à partir de l’ensemble des mesures élémentaires qui correspondent aux paires de photons émis suivant une même direction de l’espace. Tout photon entrant dans la chaîne de détection (cristaux scintillateurs couplés à des tubes photomultiplicateurs) est analysé individuellement. Il échange tout ou partie de son énergie (effet photoélectrique ou effet Compton) avec les électrons du cristal engendrant un phénomène de scintillation. L’énergie lumineuse créée, proportionnelle à l’énergie déposée, dirigée par un guide de lumière vers le photomultiplicateur entraîne une impulsion électrique. Cette impulsion électrique est proportionnelle à l’énergie lumineuse incidente.
Les principales caractéristiques de performance d’un cristal scintillateur sont :
- un coefficient d’atténuation linéaire élevé couplé à une photofraction élevée (probabilité que l’interaction dans le cristal soit un effet photoélectrique).
- un rendement de scintillation élevé.
- une faible constante de décroissance (temps mort dû à la scintillation court).
Théoriquement la désintégration de l'émetteur de positons se traduit par l'émission de rayons gamma selon une ligne permettant de retrouver les coordonnées de l'émission, mais il faut apporter certaines restrictions à cette théorie :
- le positon parcourt une petite distance avant d'être annihilé : pour le fluor 18 la résolution qui en découle est de 0,22 pour la FWHM (full width at half maximum = largeur a mi-hauteur de la fonction de dispersion linéique).
- les photons émis de l'annihilation de la paire positon-électron ne sont pas exactement à 180°. La variation angulaire de l'émission gamma est de 0,35 FWHM ce qui correspond pour des têtes espacées de 60 cm à une erreur de translation de 0,8 mm au centre du champ (FOV).
Les événements coïncidents détectés peuvent avoir 3 origines :
- coïncidence vraie : photons issus directement de la désintégration β+ détectés soit par effet photoélectrique, soit par effet Compton à l’intérieur du cristal (280-340 keV).
- coïncidence diffusée (un ou les deux photons d’annihilation changent de direction et perdent un peu d'énergie après une ou plusieurs interactions Compton dans le corps humain (170-200 keV).
- coïncidence fortuite ou aléatoire : l'arrivée en coïncidence des deux photons est due au hasard ; ils ne sont pas issus de la même désintégration β+ : les photons sont issus de sources de positons différentes arrivant en même temps sur les détecteurs.
Les événements diffusés et aléatoires altèrent la résolution et le contraste. La fraction de diffusé dépend de :
- la fenêtre énergétique d'acceptance.
- la géométrie du système.
- le morphotype du patient.
- la position des détecteurs.
- le modèle de caméra.
Les événements aléatoires dépendent de :
- la fenêtre temporelle de coïncidence .
- la distance entre les détecteurs.
- le taux de comptage (si le taux de comptage augmente, les événements aléatoires augmentent).
Appliquer la détection de positons sur un système TEMP nécessite de surmonter certaines difficultés en rapport notamment avec la faible capacité de taux de comptage qu'il faut améliorer.
Il faut donc :
a- optimiser le cristal de détection:
Il s'agit d'un cristal d'iodure de sodium dont l'épaisseur est augmentée à 19 mm ce qui double la capacité de détection en haute énergie (511 keV) par rapport à un cristal mince de 9,5 mm. Le rendement de comptage passe de 12 % pour un cristal de 9,5 mm d'une caméra TEMP standard à 26 % avec seulement une petite baisse de la résolution pour les faibles énergies (Figure 3-1). En fait, la résolution des gamma caméras dépend davantage de la qualité des collimateurs que de l’épaisseur du cristal et nous avons pu remarquer sur notre TEDC que la résolution en Médecine Nucléaire conventionnelle était peu altérée.
Figure 3-1 : Capacité de de détection du cristal de NaI
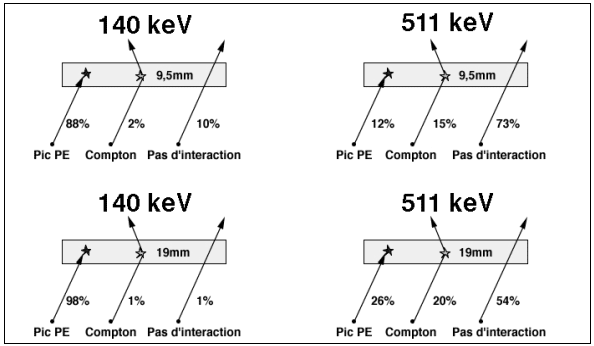
b - optimiser le nombre d'événements en coïncidence détectés en fonction de la fenêtre prise sur le spectre énergétique :
- en acceptant uniquement les pics photoélectriques de 511 keV avec une fenêtre appropriée
- en acceptant le front Compton entre 280 et 340 keV : certains photons gamma appartenant à une coïncidence vraie peuvent être partiellement absorbés à l’intérieur de cristal et peuvent être pris en compte pour augmenter le nombre de coïncidences détectées. Cette absorption Compton dans le cristal correspond à des événements détectés entre 280 et 340 keV alors que les photons diffusés par le corps du patient se situe plus volontiers entre 170 et 200 keV. Cependant, accepter les photons détectés entre 280 keV et 340 keV augmente le nombre de coïncidence vraie mais également dans un rapport moindre le nombre de coïncidences diffusées et fortuites.
c - optimiser le taux de comptage :
- en réduisant au maximum le temps mort des têtes de détection en prenant par exemple en compte uniquement la partie ascendante des impulsions et en partageant le cristal. Cette diminution du temps mort permet d’augmenter le taux de comptage mais également de minimiser les effets d’empilements (effet de sommation spectrométrique). Le circuit électronique est par ailleurs adapté pour éviter cet effet d’empilement : il rejette les événements au-delà d’un seuil de taux de comptage ne permettant plus au système de revenir à l’état basal avant l’arrivée de l’événement suivant.
- en adaptant la fenêtre de coïncidence : celle-ci est comprise entre 8 et 20 ns selon les caméras (15 ns pour la caméra Picker Axis).
- en réduisant le diffusé : pour réduire le diffusé on peut optimiser l'activité injectée et l'espacement entre les détecteurs (plus on écarte les têtes de caméra, moins on prend de diffusé local, mais plus on prend de diffusé provenant des régions du corps hors champs). C’est pourquoi les constructeurs préconisent l’utilisation d’un filtre axial comportant des septas (acquisition 2D).
3.1.2 Collimation électronique : réarrangement des données
L’acquisition des données en mode coïncidence se fait sans collimateur et pour un angle de rotation donné des têtes de caméra, les événements mesurés correspondent à des angles de projections différentes.
Pour remettre ces événements dans des projections orthogonales de manière à utiliser les programmes de reconstruction tomographique soit de type rétroprojection filtrée soit de type itératif, il est nécessaire de trier toutes les données : c’est le réarrangement des données ou « rebinning ».
En reconstruction 2D : le réarrangement des données se fait dans la direction axiale afin de définir les différents plans de coupe mais également dans les plans transverses en recombinant les événements mesurés de chaque plan en projections orthogonales.
3.1.3 Le réarrangement axial :
Il consiste à considérer que tous les événements détectés sous un angle inférieur à un angle appelé « angle d’acceptance », arrivent perpendiculairement sur les têtes de détection (Figure 3-2).
L’une des principales conséquences de cette approximation est que la résolution est meilleure au voisinage de l’axe de rotation que sur les bords du volume d’exploration. L’angle d’acceptance doit être petit et ne dépasse pas en général 16°.
Figure 3-2 : Réarrangement axial

3.1.4 Le réarrangement transverse:
Figure 3-3 : Réarrangement transverse.
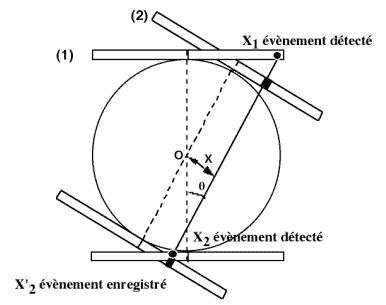
Soient X1 et X2 les événements détectés en coïncidence sur les deux têtes placées à 180°, la ligne X1X2qui correspond à la direction d’émission des deux gammas de 511 keV qui font suite à l’annihilation du positon fait un angle θ avec la perpendiculaire au plan des deux cristaux et est à une distance x du centre de rotation. Pour classer tous les événements en coïncidence en projection orthogonale, il suffit de classer et de regrouper les événements coïncidents en fonction de θ en replaçant chacun d’entre eux à une distance x du centre de rotation. Ainsi le nombre de projections orthogonales utilisables pour la reconstruction en rétroprojection filtrée ou en mode itératif est fonction de l’échantillonnage θ et non pas du nombre de projections définies à l’acquisition.
Dans le plan transverse, il est possible de limiter l’angle θ à un angle d’acceptance maximum( Figure 3-3) . Sa valeur est limitée par la largeur du champ utilisée dans la direction transverse. La valeur conseillée par le constructeur est de 480 mm c’est-à-dire la quasi-totalité du champ. Des valeurs plus faibles devraient améliorer en principe la résolution transverse
Dans le mode d’acquisition 2D, un collimateur à lames (comportant des septas interplans) permet de limiter le rayonnement diffusé en provenance du cerveau et de la vessie. Il contribue également à limiter l’angle d’acceptance des photons.
En reconstruction 3D : cette étape de « rebinning » est faite dans les directions transverse et axiale. Cependant la translation simultanée des coordonnées de ces photons dans les deux direction (en 3D) demande un temps de traitement informatique important.
La reconstruction 3D augmente la sensibilité car elle prend en compte la quasi-totalité des événements détectés en coïncidence mais en contrepartie il y a une augmentation relative des événements diffusés et aléatoires. Ce type de reconstruction existe sur des caméras TEP et commence à apparaître sur TEDC.
Les calculs de la collimation électronique peuvent être faits pendant l’acquisition en fixant au préalable les paramètres du réarrangement (conditions spectrométriques, angle d’acceptance souhaité, proportion du cristal utilisé à la détection, nombre de projections orthogonales) ou à posteriori si l’acquisition est faite en mode liste. Dans ce cas, il est possible de choisir différents paramètres de réarrangement sur une même acquisition.
3.1.5 Correction géométrique
La sensibilité de l’imagerie avec coïncidence et collimation électronique varie selon la position des événements dans le champs.
Elle varie avec la géométrie des détecteurs, l’angle de détection et les directions transverse ou axiale (Figures 3-4 et 3-5). En conséquence, une correction géométrique doit être apportée aux données brutes. Sans cette correction, le centre de l’image apparaît intense, foncé, flou et les bords clairs à peine visibles.
Dans les plans transverses, la sensibilité est maximale au centre du champ.
Figure 3-4 :Variation de la sensibilité dans le plan transverse
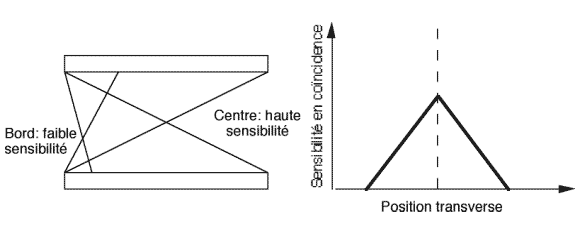
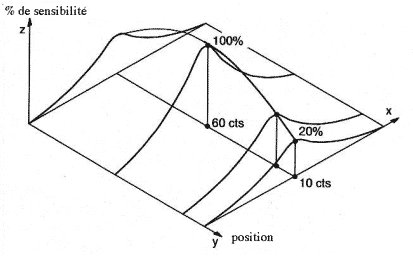
Dans la direction axiale, un angle d’acceptance étant imposé, il y a aplatissement du profil de sensibilité.
Figure 3-5 : Variation de la sensibilité dans le plan axial
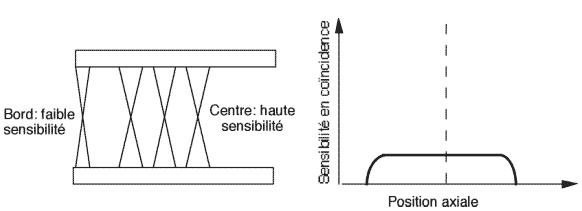
En conséquence, les variations de sensibilité doivent être corrigées par un facteur ramenant les pixels des bords au même niveau de sensibilité que ceux du centre du champ.
La correction géométrique normalise tous les pixels en fonction des probabilités géométriques d’acceptance des événements sont pris en compte l’espacement des têtes, les dimensions du champ, l’angle de rotation des têtes, la présence ou non d’un filtre axial, l’angle d’acceptance pour le « rebinning ».
Figure 3-6 : Correction de la sensibilité
La correction géométrique a cependant des limites et des inconvénients : même si on corrige à posteriori par un facteur les variations de sensibilité de comptage entre le centre et les bords du champ, la statistique de comptage (nombre de coups effectivement enregistrés) est défavorable sur les bords .(Figure 3-6). Les taux de comptage ne sont quantitativement pas corrects malgré la normalisation : il y a inexactitude de la quantification
3.1.6 Modes d’acquisition : mode liste, fenêtres spectrales
L’acquisition sur un fichier mode liste (dans lequel sont stockées les coordonnées spatiales de détection des photons ainsi que leur paramètre énergétique) permet ensuite de faire varier les paramètres du réarrangement que sont les angles d’acceptance (en axial et en transverse) mais également le choix spectrométrique.
En faisant varier les fenêtres spectrales, on peut faire varier le compromis sensibilité-résolution en choisissant :
- le mode pic-pic (PP) : seuls les événements correspondant à des photons enregistrés dans la fenêtre du pic photoélectrique sur les deux têtes sont retenus.
- le mode pic-compton (PC) : au moins un des deux photons coïncidents a été enregistré dans la fenêtre du pic photoélectrique, le second pouvant appartenir à la fenêtre spectrale du diffusé. Les événements correspondant à des photons enregistrés dans la fenêtre du diffusé sur les deux détecteurs sont rejetés.
le mode haute sensibilité (HS) : tous les événements coïncidents sont retenus quelle que soit leur énergie.
3.1.7 La reconstruction itérative
La méthode de reconstruction classique par rétroprojection filtrée amplifie le bruit statistique et en cas de fixation très intense génère des artéfacts. Ces problèmes peuvent êtres évités grâce aux algorithmes de reconstruction itératifs.
Ces méthodes itératives de reconstruction consistent à déterminer par approximations successives les valeurs du contenu de chaque pixel du plan de coupe en optimisant les différences entre les valeurs mesurées et les valeurs calculées des éléments de projection. Les critères d’optimisation diffèrent d’une méthode à l’autre.
Actuellement, les algorithmes itératifs de reconstruction les plus utilisés en détection par coïncidence sont :
- l’algorithme EM-ML (Expectation Maximization Maximum Likelihood).
- l’algorithme OSEM ou OS EM-ML (Ordered Subset Expectation Maximisation)
- les algorithmes de type ART (Algebraic Reconstruction Techniques : méthodes additives ou multiplicatives)
En ce qui concerne notre système, ce sont les méthodes EM-ML et OS EM-ML qui sont utilisées.
- L’algorithme EM-ML est auto normalisant. Il a été montré qu’il convergeait vers une image selon le critère du « maximum de vraisemblance ». Cependant cette image est construite avec des données qui contiennent le bruit et ce dernier apparaît sur celle-ci. Ce phénomène apparaît si le nombre d’itérations est trop important. C’est pourquoi ce type d’algorithme doit bénéficier d’un critère d’arrêt optimisé (20 itérations sur le système Odyssey ).
- L’algorithme OS EM-ML consiste à diviser chaque itération en sous-ensembles qui correspondent chacun à un angle de projections. Les sous-ensembles sont traités dans un ordre qui correspond à des angles de projections très différents. Une itération OS EM-ML utilise tous les sous-ensembles de projection une fois. Il a été montré qu’un petit nombre d’itérations (6 itérations sur le système Odyssey) conduisait à un résultat équivalent à l’algorithme EM-ML. Cependant la méthode n’est pas auto-normalisante et chaque itération est ralentie car les facteurs de normalisation sont calculés en vol.
3.1.8 Les filtres de convolution
Les hautes fréquences de l’image correspondent à la fois au bruit de fond, mais aussi aux petites structures et aux contours fins de l’image.
Quatre filtres de convolution sont disponibles dans la station de traitement d’image :
Deux filtres utilisent la fonction de transfert de modulation du système Axis : le filtre de METZ et le filtre de WIENER. Ils permettent d’augmenter sensiblement la résolution et le contraste lors de la suppression du bruit.
Le filtre de METZ est dépendant du nombre de coups
H(f) = 1 / (MTF(f)) x [ 1 – ( 1 – (MTF(f)2))x]
où MTF (f) est la valeur de la fonction de transfert de modulation à une fréquence donnée et x un facteur qui contrôle l’atténuation des hautes fréquences.
Le filtre de WIENER est nombre de coups indépendant.
H(f) = MTF(f) / [ MTF(f)2 + 1 /SNR(f) ]
où SNR(f) = valeur du spectre de l’objet à la fréquence f / [ valeur du spectre du bruit à la fréquence f x multiplicateur du bruit).
Dans l’étude qui suit nous avons utilisé le filtre de WIENER qui est nombre de coups indépendant et d’utilisation plus facile en clinique.
3.2 Principe d’optimisation de la caméra TEDC
3.2.1 Les paramètres d’évaluation d’une caméra TEDC
Les principales performances des systèmes de détection à coïncidence sont la résolution spatiale, la sensibilité et le taux de comptage. Différents protocoles de mesures ont été développés pour comparer les performances mesurées sur les gamma-caméras TEDC par rapport aux caméras TEP. Il est en effet nécessaire de respecter autant que possible les mêmes conditions de mesure des différents paramètres d’évaluation en suivant au plus près les normes NEMA établies pour les caméras TEP (NEMA NU1. Performance measurements of positron emission tomographs.1994; National Electrical Manufacturers Association, Washington DC).
3.2.2 La résolution spatiale
La résolution spatiale est définie comme la capacité à séparer deux sources voisines. Elle peut être mesurée par la largeur à mi-hauteur (LMH) de la fonction de dispersion linéique, c’est-à-dire de la réponse impulsionnelle du système. Il est cependant intéressant de connaître la fonction de dispersion linéique dans sa globalité. Les queues de distribution de cette fonction (reflétées par la mesure de la largeur au dixième de la hauteur (LDH) donnent davantage de renseignement sur les pertes de contraste. Pour cela on utilise une source linéaire : fil radioactif dont on étudie la réponse impulsionnelle dans la direction orthogonale à l’axe du fil en répétant la mesure pour plusieurs orientations du fil.
En pratique, il est recommandé (normes NEMA) d’utiliser une source linéaire remplie de 18F et placée au centre d’un cylindre de 20 cm de diamètre rempli d’eau. Ce fantôme doit être étudié en différents endroits du champ et notamment dans le sens axial et le plan transverse
3.2.3 La sensibilité
La sensibilité du système représente le nombre de photons détectés par rapport au nombre de photons émis. Elle dépend de la géométrie de la source, du milieu plus ou moins atténuant (morphotype du patient), de l’angle solide de détection (mode d’acquisition 2D ou 3D) et de l’efficacité intrinsèque du détecteur.
Les normes NEMA recommandent l’utilisation d’un fantôme cylindrique de 20 cm de diamètre contenant une activité suffisamment faible pour éviter un biais de saturation du détecteur. On utilise une concentration d’activité de 3,7 kBq/ml (soit 0,1 µCi/ml).. On mesure le rapport entre l’activité de la source enregistrée par la caméra (en coups par seconde) et le comptage réel de la source (en Bq/ml) dans un compteur puit.
3.2.4 Taux de comptage. Courbes NEC
Le taux de comptage définit la relation entre l’activité mesurée par la caméra et la radioactivité réellement présente dans le champ de détection.
Soient :
- Nv le taux de coïncidences vraies.
- Na le taux de coïncidences aléatoires.
- Nd le taux de coïncidences diffusées.
Les taux sont fonction de la concentration radioactive de la solution dans le fantôme.
Le NEC (Noise Equivalent Count Rate) équivaut au rapport signal sur bruit à l’acquisition :
NEC = Nv2 / [Nv + Nd + k.Na]
où k est un facteur géométrique qui dépend de la taille du champ de la caméra.
Pour mesurer ces paramètres on utilise un fantôme cylindrique de 20 cm de diamètre et 20 cm de haut rempli initialement avec une activité suffisante proche des performances maximales de taux de comptage de la caméra. Des acquisitions avec évaluation des taux de comptage sont effectuées à intervalles réguliers au cours du temps. Pour chacune de ces mesures sont calculés Nv, Na et Nd. La courbe NEC obtenue reflète l’évolution du taux de comptage en fonction de l’activité présente dans le champ (décroissante au cours du temps). En pratique, calculer Nv, Nd, et Na n’est pas simple. Différentes méthodes ont été utilisées plus ou moins sophistiquées en fonction des caméras étudiées et des logiciels spécifiques ont été mis au point à cet effet (10).
Les performances en matière de taux de comptage dépendent :
3.2.5 La détectabilité.
La détectabilité est la capacité de détecter de petites structures hyperfixantes en fonction de leur taille et du contraste. C’est un paramètre particulièrement important en oncologie ou il est nécessaire de connaître les limites de détectabilité des tumeurs en fonction de leur taille et du contraste.
D’après les données de la littérature, le contraste entre tumeur et muscle est généralement compris entre 1 et 2 pour les tumeurs bénignes et entre 2 et 10 pour les tumeurs malignes (14). Dans ces conditions, la taille minimale des lésions vues en TEP est de 5 mm de diamètre, mais il est évident que cette taille dépend de l’activité spécifique de la lésion.
Pour évaluer la détectabilité on utilise un fantôme de sphères hyperfixantes de diamètres différents connus dont on peut faire varier la concentration en activité et le contraste par rapport au reste du fantôme. On étudie alors la restitution du contraste en comparant le contraste mesuré par la machine au contraste réel déduit des paramètres de remplissage des sphères.
le contraste réel s’exprime par :
C réel = (Activité spécifique des sphères – Activité spécifique de remplissage) / Activité spécifique de remplissage.
le contraste mesuré s’exprime par :
C mesuré = (Nb de coups par pixel des sphères – Nb de coups par pixel de remplissage) / Nb de coups par pixel de remplissage.
Le choix du contraste peut être orienté par l’intérêt clinique avec notamment un seuil de contraste critique intéressant autour de 2. Les mesures de détectabilité effectuées par O. de Dreuille (10) ont été faites avec un contraste de 2.7.
3.3 Matériel et méthodes
L’objectif de notre travail n’a pas été d’évaluer les caractéristiques de notre caméra CEDT mais de mesurer un certain nombre de paramètres pour en faire la meilleure utilisation possible en fonction des paramètres d’acquisition : angles d’acceptance axial et transverse, conditions spectrométriques, méthodes de traitement, etc … C’est pourquoi ne disposant pas encore des fantômes nécessaires pour mesurer la résolution, la sensibilité selon les normes NEMA, nous avons effectué nos mesures avec un matériel et des procédures légèrement différentes.
Cette étude est essentiellement centrée sur la recherche d’un compromis entre résolution, taux de comptage et détectabilité en fonction des paramètres d’acquisition et des traitements d’image utilisés.
3.3.1 Le taux de comptage
Nous avons utilisé une source linéaire de 18FDG obtenue à l’aide d’un cathéter de 0,92 mm de diamètre et de 30 cm de long. Les activités utilisées ont été de l’ordre de 13 MBq (350 µCi environ).
Le cathéter a été placé dans l’air au voisinage du centre de rotation dans la direction axiale. L’acquisition des données est faite en mode liste de manière à pouvoir varier les paramètres dont dépendent le taux de comptage (spectrométrie, transacceptance et angle d’acceptance). Deux acquisition ont été réalisées pour étudier l’effet de la distance des têtes au centre de rotation. Deux distances ont été testées : 25 cm correspondant à la distance minimale utilisable (patient très mince) et 35 cm correspondant à la distance maximale d’utilisation.
Les résultats obtenus sont exprimés dans le Tableau 3-1 en prenant comme référence du taux de comptage celui qui correspond à une spectrométrie pic-pic à 20%, une transacceptance de 480 mm, un angle d’acceptance θ de 16° et une distance des têtes au centre de rotation de 35 cm.
Comme le montre le tableau 3-1, le taux de comptage peut varier dans un rapport de 1,7 en fonction des paramètres d’acquisition. Il dépend beaucoup des valeurs de la transacceptance et de l’angle d’acceptance et un peu moins des conditions spectrométriques.
Comme nous le verrons dans les paragraphes suivants, augmenter le taux de comptage n’augmente pas forcément la résolution et la détectabilité car il y a augmentations conjointes des nombres de coïncidences diffusées et fortuites et donc du bruit de fond.
| Distance axe de rotation/têtes = 35cm | ||||
| Spectrométrie | Pic-Pic 20% | Pic-Pic 30% | Pic-Compton 30% | Haute sensibilité |
| Transacceptance de 480 mm et θ de 16° | 1,00 | 1,12 | 1 ,73 | 2,10 |
| Transacceptance de 480 mm et θ de 8° | 0,89 | 0,98 | 1,49 | 1,52 |
| Transacceptance de 480 mm et θ de 4° | 0,62 | 0,69 | 1,03 | 1,22 |
| Transacceptance de 240 mm et θ de 16° | 0,55 | 0,62 | 0,95 | 1,18 |
| Transacceptance de 120 mm et θ de 16° | 0,29 | 0,32 | 0,49 | 0,61 |
| Distance axe de rotation/têtes = 25cm | ||||
| Spectrométrie | Pic-Pic 20% | Pic-Pic 30% | Pic-Compton 30% | Haute sensibilité |
| Transacceptance de 480 mm et θ de 16° | 1,25 | 1,40 | 2,16 | 2,66 |
| Transacceptance de 480 mm et θ de 8° | 1,10 | 1,21 | 1,84 | 2,22 |
| Transacceptance de 480 mm et θ de 4° | 0,76 | 0,84 | 1,27 | 1,51 |
| Transacceptance de 240 mm et θ de 16° | 0,72 | 0,81 | 1,25 | 1,57 |
| Transacceptance de 120 mm et θ de 16° | 0,38 | 0,43 | 0,66 | 0,83 |
3.3.2 La résolution
Nous avons utilisé une source linéaire de 18FDG obtenue à l’aide d’un cathéter de 0,92 mm de diamètre et de 30 cm de long. Les activités utilisées ont été de l’ordre de 13 MBq (350 µCi environ). Le cathéter a été placé dans l’air au voisinage du centre de rotation dans la direction axiale pour mesurer la résolution transverse et dans une direction transverse pour mesurer la résolution axiale. Les mesures ont été répétées pour deux rayons de rotation différents : 25 et 35 cm. Des mesures du même type ont été effectuées avec la source placée à 20 cm du centre de rotation. Les enregistrements ont été faits en mode liste ce qui nous a permis de varier les paramètres d’acquisition et de traitement sur une même acquisition.
La mesure des résolutions LMH et LDH est automatique à l’aide d’un programme qui moyenne celle-ci sur une longueur de 16 pixels.
Les conditions spectrométriques utilisées sont les suivantes :
- mode pic-pic avec fenêtres de 20%
- mode pic-pic avec fenêtres de 30%
- mode pic-compton avec fenêtres de 30%
- mode haute sensibilité (280 à 620 keV)
Les deux algorithmes de reconstruction itérative OS EM-ML et EM-ML ont été testés.
L’influence des valeurs de la « transacceptance » et des angles d’acceptance a également été étudiée.
L’influence du filtre de WIENER sur la résolution a été étudiée avec plusieurs valeurs du coefficient multiplicatif : 0,10 - 0,30 - 0,50 et 0,69.
Les résultats obtenus sont consignés dans les tableaux 5 à 16.
Tableau 3-2 : Résolution axiale au voisinage du centre de rotation/Acquisition pic/pic
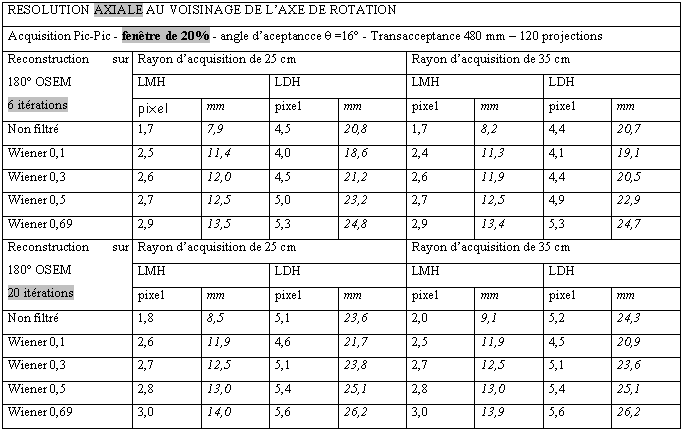
Tableau 3-3 : Résolution axiale au voisinage du centre de rotation/Acquisition pic/pic
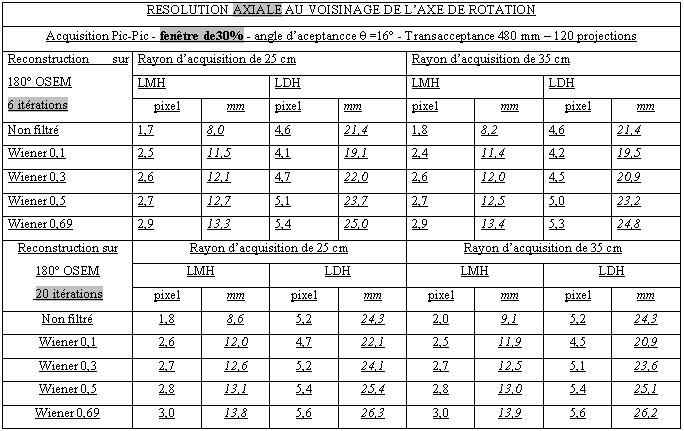
Tableau 3-4 : Résolution axiale au voisinage du centre de rotation/Acquisition pic/Comton
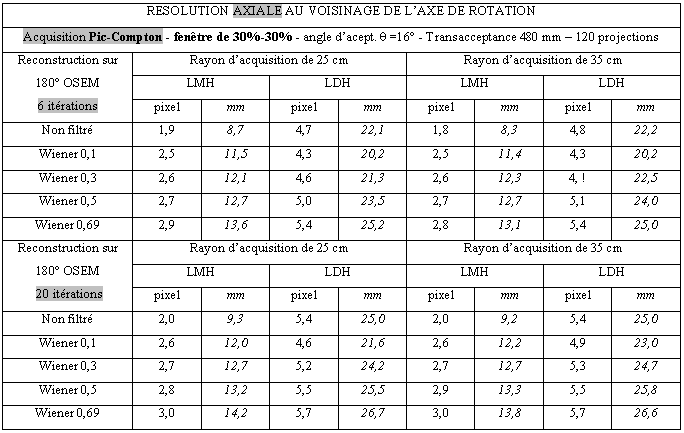
Tableau 3-5 : Résolution axiale au voisinage du centre de rotation/ Haute sensibilité
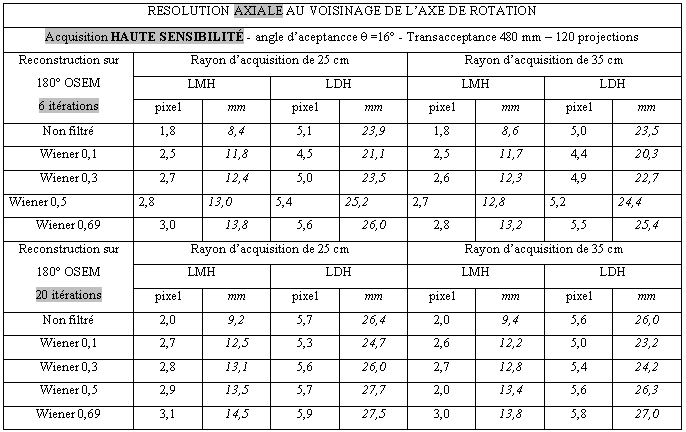
Tableau 3-6 : Résolution axiale au voisinage du centre de rotation/Acquisition pic/pic/θ = 8°
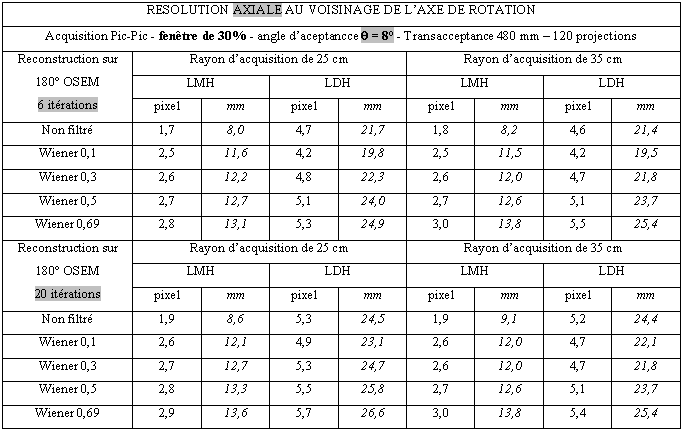
Tableau 3-7 : Résolution axiale au voisinage du centre de rotation/Acquisition pic/pic/Ф= 8°
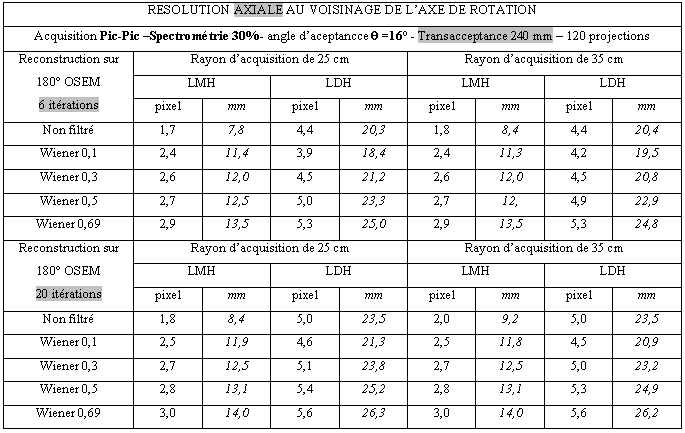
Tableau 3-8 : Résolution transverse au centre de rotation/Acquisition pic/pic

Tableau 3-9 : Résolution transverse au centre de rotation/Acquisition pic/Compton
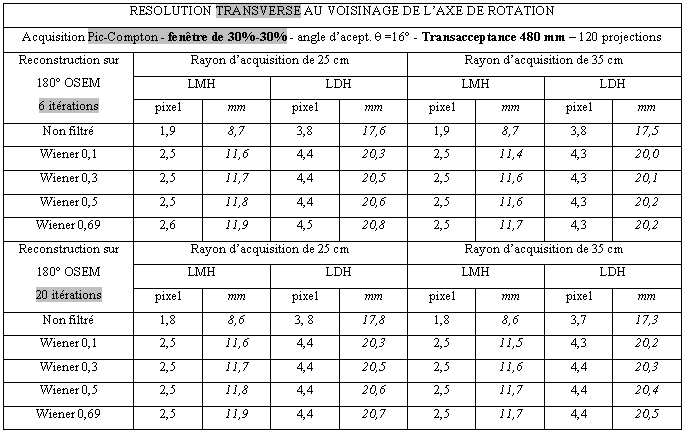
Tableau 3-10 : Résolution transverse au centre de rotation/Haute sensibilité
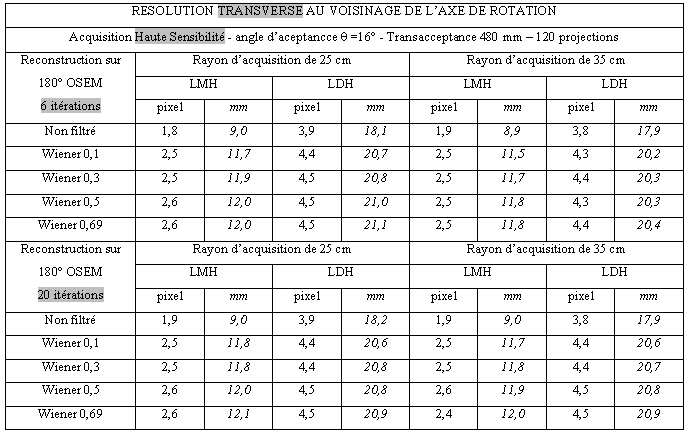
Tableau 3-11 : Résolution transverse au centre de rotation/ Acquisition pic/pic/θ= 8°
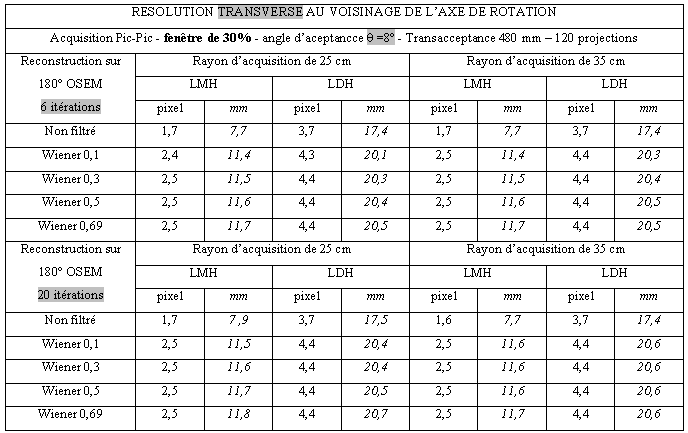
Tableau 3-12 : Résolution transverse au centre de rotation/ Acquisition pic/pic/Ф= 240mm
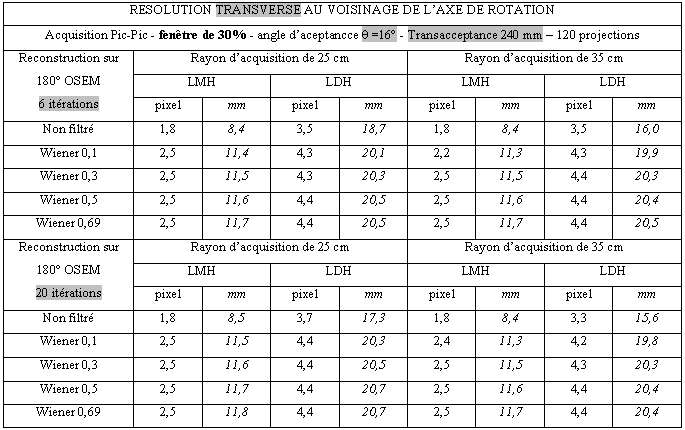
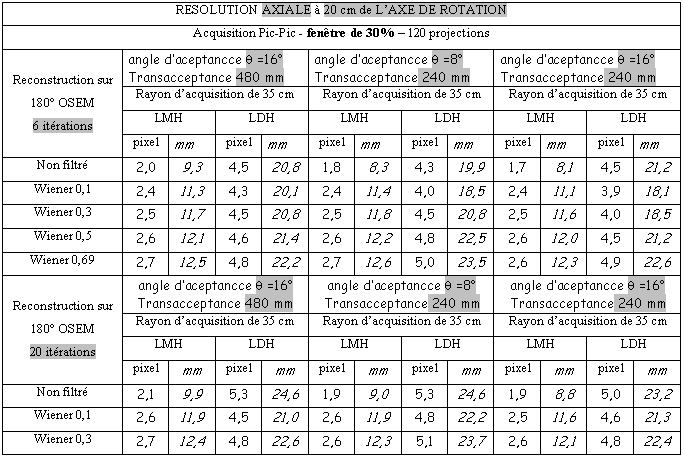
Tableau 3-13 :Résolution axiale à 20 cm du centre de rotation/ Acquisition pic/pic
3.4 Discussion :
Les résolutions obtenues LMH et LDH peuvent être comparées en fonction des différents paramètres par le test « t » des séries appariées.
En fonction de la spectrométrie et des acceptances: le test « t » est appliqué en fonction des différentes conditions spectrométriques et des différentes acceptances.
3.4.1 La résolution axiale :
Les résultats statistiques obtenus sont consignés dans le tableau 17.
| Comparaison des acquisitions | Différence des moyennes en mm | p | significativité |
| Largeur à mi-hauteur (LMH) | |||
| PP20% θ =16°/ PP30% θ =16° | - 0,045 | 0,035 | Peu S |
| PP30% θ =16°/ PC30% θ =16° | - 0,165 | < 0,008 | S |
| PC30% θ =16°/ H. Sensibilité θ =16° | - 0,170 | < 0,0007 | S |
| PP30% θ =16°/ PP30% θ =8° | -0,010 | 0,827 | NS |
| PP30% 480mm / PP30% 240mm | 0,015 | 0,603 | NS |
| Largeur au dizième de la hauteur (LDH) | |||
| PP20% θ =16°/ PP30% θ =16° | - 0,315 | < 0,001 | S |
| PP30% θ =16°/ PC30% θ =16° | - 0,550 | < 0,002 | S |
| PC30% θ =16°/ H. Sensibilité θ =16° | - 0,985 | < 0,0001 | S |
| PP30% θ =16°/ PP30% θ =8° | 0,165 | 0,335 | NS |
| PP30% 480mm / PP30% 240mm | 0,195 | < 0,0002 | S |
Il existe donc une diminution significative des résolutions LMH et LDH lorsque l’on utilise le rayonnement diffusé ou le mode « haute sensibilité ». Par contre les différences de résolutions sont peu significatives lorsque l’on utilise une spectrométrie pic-pic et des fenêtres de 20 % et 30 %.
Les améliorations de résolution espérées en diminuant les angles d’acceptance (axial et transverse) ne sont pas significatives par rapport à la spectrométrie pic-pic correspondante. Compte tenu des pertes de comptage induites par la diminution de ces angles, cette possibilité ne doit pas être utilisée.
3.4.2 La résolution transverse:
Les résultats statistiques obtenus sont consignés dans le tableau 3-16.
| Comparaison des Acquisitions | Différence des moyennes en mm | p | significativité |
| Largeur à mi-hauteur (LMH) | |||
| PP20% θ =16°/ PP30% θ =16° | - 0,030 | 0,368 | N S |
| PP30% θ =16°/ PC30% θ =16° | - 0,080 | 0,012 | Peu S |
| PC30% θ =16°/ H. Sensibilité θ =16° | - 0,200 | < 0,0001 | S |
| PP30% θ =16°/ PP30% θ =8° | 0,160 | 0,042 | N S |
| PP30% 480mm / PP30% 240mm | 0,055 | 0,012 | N S |
| Largeur au dizième de la hauteur (LDH) | |||
| PP20% θ =16°/ PP30% θ =16° | - 0,195 | 0,184 | N S |
| PP30% θ =16°/ PC30% θ =16° | - 0,140 | 0,055 | N S |
| PC30% θ =16°/ H. Sensibilité θ =16° | - 0,305 | < 0,0001 | S |
| PP30% θ =16°/ PP30% θ =8° | - 0,150 | 0,019 | Peu S |
| PP30% 480mm / PP30% 240mm | 0,045 | 0,709 | N S |
La résolution transverse semble moins sensible aux conditions spectrométriques. Là encore les diminutions des angles d’acceptance n’améliore pas la résolution de manière très significative.
Compte tenu de ces résultats, en résolution spatiale axiale et transverse, l’utilisation de fenêtres spectrométriques de 30 % centrées sur le pic photoélectrique semble un bon compromis car elles permettent une amélioration sensible des taux de comptage.
3.4.2.1 En fonction de la distance des têtes à l’axe de rotation :
Les résolutions axiales et transverses dépendent t-elles de la distance des têtes à l’axe de rotation ? Si ce problème est évident en médecine nucléaire conventionnelle, le problème l’est moins en détection par coïncidence.
Là encore on applique le test « t » des séries appariées sur les données brutes des résolutions brutes LMH et LDH pour résoudre le problème. Les résultats sont retranscrits dans le tableau 3-17.
| Comparaison 25cm / 35cm | Différence des moyennes en mm | p | significativité |
| Résolution axiale LMH | 0,033 | 0,394 | N S |
| Résolution axiale LDH | 0,675 | 0,051 | N S |
| Résolution transverse LMH | - 0,308 | 0,008 | S |
| Résolution transverse LDH | 0,033 | 0,698 | N S |
Ces résultats nous conduisent à conclure que les résolutions axiales et transverses sont indépendantes de la distance à l’axe de rotation. Ainsi, on pourra choisir de passer au plus près du patient de manière à augmenter le taux de comptage sans à priori modifier la résolution.
3.4.2.2 En fonction du programme de reconstruction :
les programmes de reconstruction itératifs OS EM-ML avec 6 itérations et EM-ML avec 20 itérations sont-ils équivalents en termes de résolution ?
Les données brutes obtenues avec les deux méthodes sont comparées avec le test « t » des séries appariées. Les résultats sont consignés dans le tableau 20.
| Comparaison OSEM/EMML | Différence des moyennes en mm | p | significativité |
| Résolution axiale LMH | - 0,742 | < 0,0001 | S |
| Résolution axiale LDH | - 2,917 | < 0,0001 | S |
| Résolution transverse LMH | - 0,050 | 0,365 | N S |
| Résolution transverse LDH | 0,342 | 0,281 | N S |
Si les différences de résolution sont très significatives en ce qui concerne les résolutions axiales LMH et LDH avec le programme OS EM-ML, il n’existe aucune différence significative sur les résolutions transverses.
3.4.2.3 En fonction du filtrage 3D appliqué après la reconstruction :
Nous avons étudié l’influence d’un filtre de WIENER sur la résolution avec différents coefficients multiplicatifs 0,10 - 0,30 – 0,50 et 0,69. Nous avons préféré le filtre de WIENER nombre de coups indépendants, au filtre de METZ nombre de coups dépendants.
Le filtre de WIENER a trois effets : un effet renforçateur de contraste car il amplifie les moyennes fréquences, un effet de suppression du bruit de fond et un effet de lissage de l’image car il atténue les basses fréquences.
L’étude de significativité est faite à l’aide du test « t » des séries appariées.
Les résultats sont exprimés dans le tableau 21.
| Comparaison des Filtres | Pic | Différence des moyennes en mm | P | Significativité |
| RÉSOLUTION TRANSVERSE | ||||
| Brut/Wiener 0,10 | LMH | - 3,017 | < 0,0001 | S |
| Wiener 0,10/Wiener 0,30 | LMH | - 0,117 | < 0,0001 | S |
| Wiener 0,30/Wiener 0,50 | LMH | - 0,092 | < 0,0001 | S |
| Wiener 0,50/Wiener 0,69 | LMH | - 0,083 | 0,0165 | Peu S |
| Brut/Wiener 0,10 | LDH | - 2,883 | < 0,0001 | S |
| Wiener 0,10/Wiener 0,30 | LDH | - 0,142 | < 0,0001 | S |
| Wiener 0,30/Wiener 0,50 | LDH | - 0,121 | < 0,0001 | S |
| Wiener 0,50/Wiener 0,69 | LDH | - 0,083 | 0,1415 | N S |
| RÉSOLUTION AXIALE | ||||
| Brut/Wiener 0,10 | LMH | - 3,171 | < 0,0001 | S |
| Wiener 0,10/Wiener 0,30 | LMH | - 0,700 | < 0,0001 | S |
| Wiener 0,30/Wiener 0,50 | LMH | - 0,429 | < 0,0001 | S |
| Wiener 0,50/Wiener 0,69 | LMH | - 0,779 | < 0,0001 | S |
| Brut/Wiener 0,10 | LDH | 2,050 | < 0,0001 | S |
| Wiener 0,10/Wiener 0,30 | LDH | - 1,792 | < 0,0001 | S |
| Wiener 0,30/Wiener 0,50 | LDH | - 1,925 | < 0,0001 | S |
| Wiener 0,50/Wiener 0,69 | LDH | - 0,983 | < 0,0001 | S |
Le filtrage de WIENER diminue de façon significative les résolutions transverses et axiales LMH et LDH sauf sur les résolutions axiales LDH avec les filtres WIENER 0,10 et WIENER 0,30 où on note une amélioration de la résolution respectivement de 2,05 mm et de 0,26 mm en moyenne.
3.4.2.4 En fonction de la situation de la source dans le champ :
Toutes les études précédentes concernent le champ central c’est-à-dire au voisinage de l’axe de rotation. Que devient la résolution pour un objet à distance de l’axe de rotation ?
Le tableau 20 montre les résultats obtenus en résolutions axiales et transverses pour une source linéaire placée à 20 cm du centre de rotation. Pour des raisons d’encombrement, celles-ci ont été estimées pour une seule distance des têtes à l’axe de rotation (R = 35 cm)
Les résultats obtenus montrent qu’il n’y a pas de différence significative entre les résolutions axiales au voisinage du centre de rotation et à distance du centre de rotation.
Par contre, il existe une différence significative des résolutions transverses (en moyenne 4,1 mm pour LMH soit une perte de l’ordre de 50% et 6,72 mm pour LDH soit une perte de l’ordre de 30%).
| Comparaison de la position de la source centre/20cm | Différence des moyennes en mm | p | significativité |
| Résolution axiale LMH | 0,183 | 0,477 | N S |
| Résolution axiale LDH | - 1,033 | 0,227 | N S |
| Résolution transverse LMH | 4,100 | < 0,0001 | S |
| Résolution transverse LDH | 6,717 | < 0,0001 | S |
3.4.3 La détectabilité.
Elle a été étudiée à l’aide d’un fantôme elliptique de R.J JASZCZAK comprenant une cuve elliptique, remplissable et étanche dont les dimensions internes sont 30,5 cm de grand axe, 22 cm de petit axe et 18,6 cm de hauteur soit un volume de 9,8 litres.
Six sphères creuses dont les diamètres internes sont respectivement 0,90 cm -1,20 cm – 1,46 cm – 2,16 cm – 2,74 cm – 3,40 cm (soient respectivement 0,38 ml – 0,90 ml - 1,60 ml – 5,20 ml – 10,89 ml –20,58 ml). Ces sphères sont vissées sur des tiges plastiques qui les maintiennent à 12,7 cm de la base du fantôme.
Figure 3-7 : Fantôme de Boules

Trois contrastes différents ont été étudiés :
- les boules ont été remplies avec une solution d’activité spécifique de 21 MBq/l (0,57 mCi/l) et le fantôme avec une solution d’activité spécifique de 8 MBq/l (0,216 mC/l). Le rapport de concentration est de 2,64 et le contraste de 1,63.
- les boules ont été remplies avec une solution d’activité spécifique de 129,5 MBq/l (3,50 mCi/l) et le fantôme avec une solution d’activité spécifique de 8,18 MBq/l (0,221 mCi/l). Le rapport de concentration est de 15,8 et le contraste de 14,9.
- les boules ont été remplies avec une solution d’activité spécifique de 69,2 MBq/l (1,87 mCi/l) et le fantôme avec une solution d’activité spécifique de 8,18 MBq (0,221 mCi/l). Le rapport de concentration est de 8,46 et le contraste de 7,5.
Les contrastes de l’image sont calculés à partir de coupes de 4 pixels d’épaisseur. Les données prises en compte sont les valeurs moyennes obtenues à partir d’un comptage en 9 points au centre des images des boules et à mi-distance du centre de deux boules voisines pour le bruit de fond. La valeur du bruit de fond retenue pour le calcul du contraste d’une boule est la moyenne des deux bruits de fond adjacents à celles-ci.
Les tableaux 3-21, 3-22, 3-23, 3-24, et 3-25 expriment les résultats mesurés dans les différentes conditions d’acquisition et de traitement déjà utilisées pour l’étude de la résolution.
Tableau 3-21 : Distance des têtes à 25 cm/ reconstruction par OSEM 6 itérations
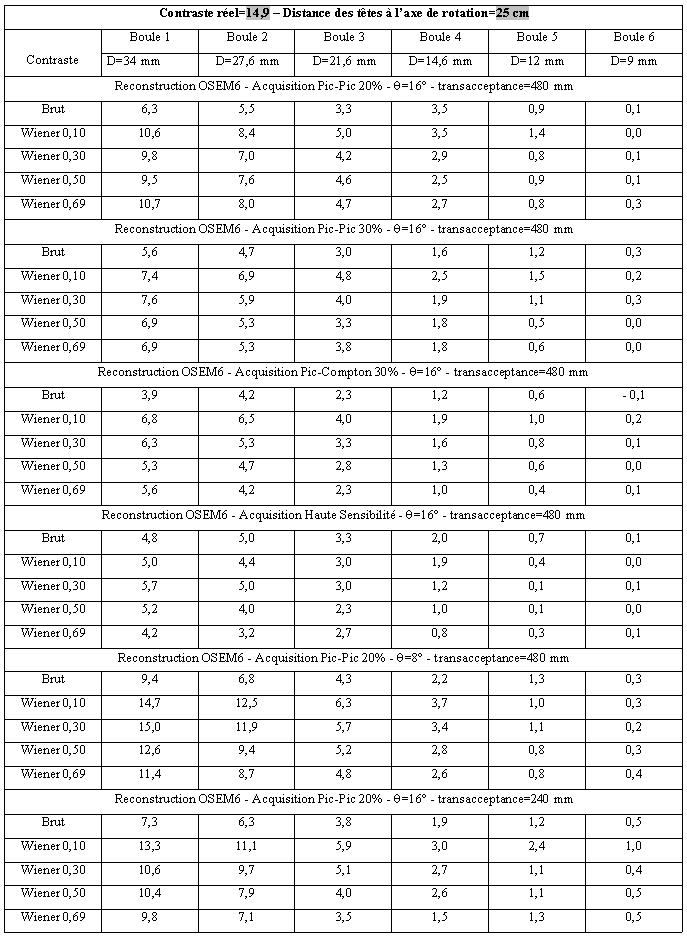
Tableau 3-22 : Distance des têtes à 25 cm/ reconstruction par EMML 20 itérations
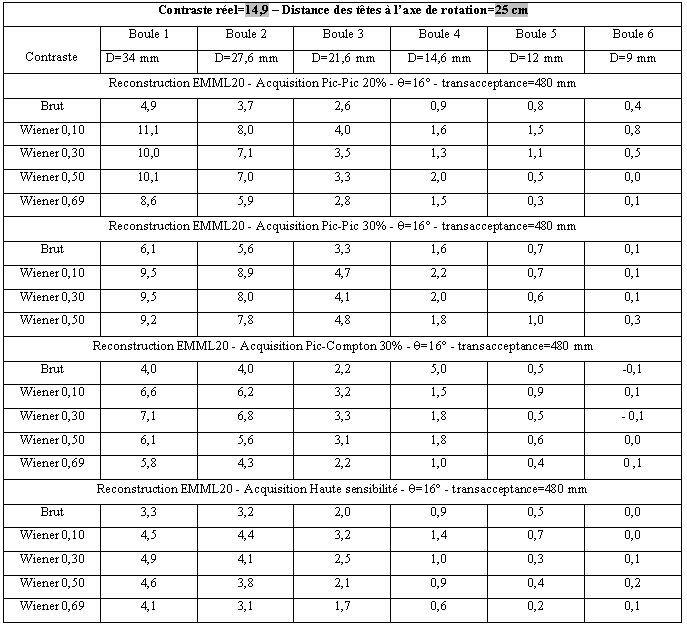
Tableau 3-23 : Distance des têtes à 35 cm/ reconstruction par OSEM 6 itérations
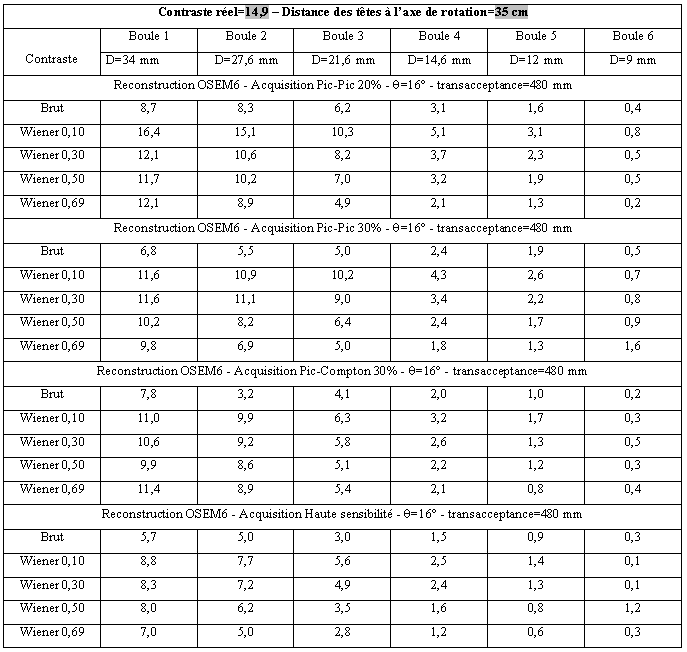
Tableau 3-24 : Distance des têtes à 35 cm/ reconstruction par EMML 20 itérations

Tableau 3-25 : Distance des têtes à 25 cm/ reconstruction par OSEM 6 itérations
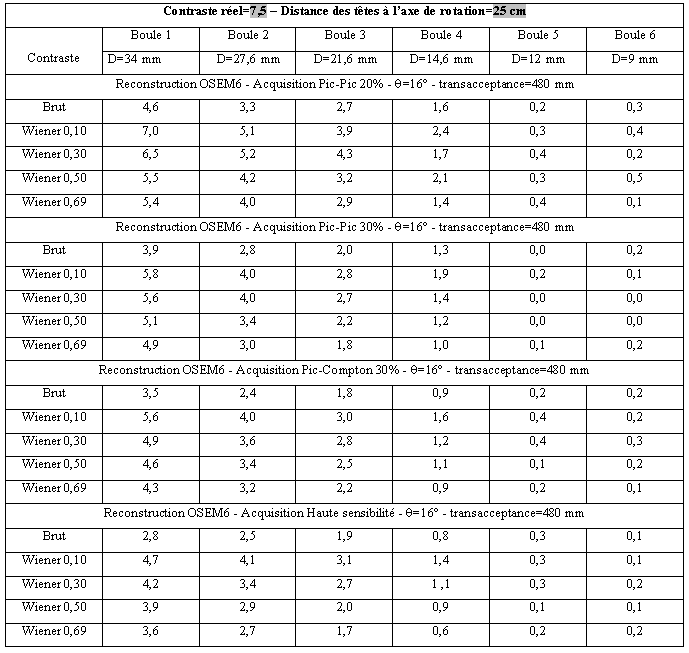
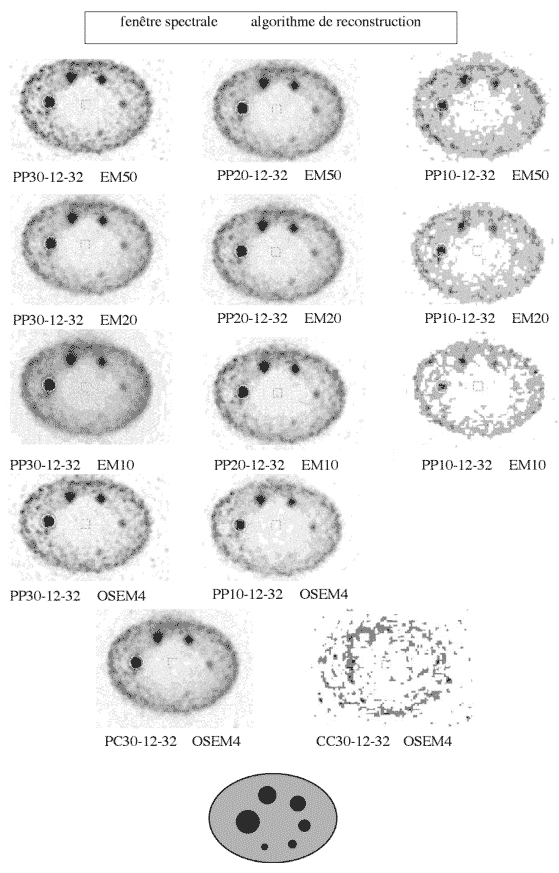
Figure 3-8 : Représentation du Fantôme à boules en fonction de la spectrométrie et de la reconstruction
3.4.3.1 Discussion :
On remarquera tout de suite une similitude entre les résultats des études de contraste et résolutions spatiales.
Les sphères sont nettement visibles pour un contraste mesuré de 1 (Figure 3-8). Au dessous de la valeur 0,7, les sphères ne sont pas visibles. Entre 0,7 et 1, il existe une zone d’incertitude où les sphères peuvent être détectables lorsque l’on connaît l’objet.
Comme dans l’étude précédente, on a utilisé le test « t » des séries appariées. Seuls les résultats obtenus avec les quatre plus grosses sphères ont été utilisés. En effet celles-ci restent toujours visibles.
3.4.3.2 En fonction des conditions spectrométriques :
Le tableau 3-26 montre les résultats des tests statistiques.
| Comparaison de la spectrométrie | Différence des moyennes en mm | p | significatif |
| PP 20% / PP 30% | 0,56 | 0,0334 | Peu S |
| PP 30% / PC 30% | 1,29 | 0,0003 | S |
| PC 20% Haute sensibilité | 0,55 | 0,0676 | N S |
On note une dégradation du contraste lorsqu’on élargit la spectrométrie. Cette dégradation est peu significative lorsque l’on passe d’une fenêtre de 20 % à 30 %, est significative lorsque l’on utilise le Compton ou le mode haute sensibilité.
Il semble exister une amélioration du contraste lorsque l’on réduit l’angle d’acceptance et la transacceptance . Il n’a pas été fait de test statistique en raison du petit nombre de données.
3.4.3.3 En fonction de la distance à l’axe de rotation :
Comme pour la résolution, les distances 25cm et 35 cm ont été testées. Le contraste est meilleur pour un rayon de 35 cm d’une valeur absolue de 1,6 en moyenne, le test « t » étant significatif à p = 0,004. La résolution n’étant pas affectée par le rayon de rotation des têtes, la baisse du contraste observé lorsqu’on rapproche les têtes est due essentiellement à une augmentation du rayonnement diffusé en provenance de l’objet.
3.4.3.4 En fonction du programme de reconstruction :
La comparaison par le test « t » des séries appariées des valeurs des contrastes obtenus avec les deux programmes de reconstruction OS EM-ML et EM-ML montrent l’obtention de meilleurs contrastes avec la méthode itérative OS EM-ML. Cependant le p=0,0214 est en faveur d’un test peu significatif.
3.4.3.5 En fonction du filtrage 3D appliqué après la reconstruction :
Le tableau 3-27 résume les tests statistiques réalisés à partir des contrastes mesurés après application des filtrages de WIENER.
| Filtrage | contraste | Rapport des Contrastes Wiener/Brut | p | Significativité |
| Boule 1 : diamètre de 34 mm | ||||
| Brut | 5,09 | |||
| Wiener 0,10 | 8,02 | 1,58 | 0,0003 | S |
| Wiener 0,30 | 7,59 | 1,49 | < 0,0001 | S |
| Wiener 0,50 | 7,02 | 1,38 | 0,0013 | S |
| Wiener 0,69 | 6,68 | 1,31 | 0,0042 | S |
| Boule 2 : diamètre de 27,6 mm | ||||
| Brut | 4,15 | |||
| Wiener 0,10 | 6,75 | 1,63 | < 0,0001 | S |
| Wiener 0,30 | 6,06 | 1,46 | < 0,0001 | S |
| Wiener 0,50 | 4,62 | 1,11 | 0,3065 | S |
| Wiener 0,69 | 4,87 | 1,17 | 0,0409 | S |
| Boule 3 : diamètre de 21,6 mm | ||||
| Brut | 3,02 | |||
| Wiener 0,10 | 4,87 | 1,61 | < 0,0001 | S |
| Wiener 0,30 | 4,16 | 1,38 | < 0,0001 | S |
| Wiener 0,50 | 3,60 | 1,19 | 0,0002 | S |
| Wiener 0,69 | 2,21 | 0,73 | 0,0184 | Peu S |
| Boule 4 : diamètre de 14,6 mm | ||||
| Brut | 1,76 | |||
| Wiener 0,10 | 2,44 | 1,39 | < 0,0001 | S |
| Wiener 0,30 | 2,04 | 1,16 | 0,021 | N S |
| Wiener 0,50 | 1,80 | 1,02 | 0,71 | N S |
| Wiener 0,69 | 1,43 | 0,81 | 0,0027 | S |
Ces résultats montrent que l’application d’un filtre de WIENER améliore le contraste. L’augmentation du contraste est maximum pour les faibles valeurs du coefficient multiplicatif (0,1 – 0,3) où les effets renforçateurs et d’abaissement du bruit de fond sont prépondérants par rapport à l’effet lissage.
Le contraste peut être multiplié par un facteur qui peut atteindre 1,6. Malheureusement cette augmentation de contraste est beaucoup plus nette pour les images qui possèdent déjà un bon contraste que pour les images peu contrastées et il n’y a pas forcément amélioration de la détectabilité.
3.5 Conclusion
Ce travail nous a permis d’évaluer de manière quantitative l’influence des paramètres d’acquisition et de traitement de notre caméra TEDC sur la qualité des images obtenues. Nous rappelons que l’objectif de ce travail n’était pas de comparer notre système aux autres systèmes existants mais d’optimiser nos procédures d’acquisition et de traitement.
Pour conclure ce chapitre, nous pouvons faire les recommandations suivantes :
- utilisation d’une fenêtre spectrométrique pic-pic 30 % : elle permet d’avoir un taux de comptage supérieur à celui obtenu avec une fenêtre de 20% sans altérer de manière trop significative la résolution et le contraste.
- ne pas utiliser la possibilité de diminuer l’ angle d’acceptance et la transacceptance car elles entraînent une diminution trop importante du taux de comptage.
- placer les têtes à distance du patient : bien qu’il n’existe pas de différence significative de résolution spatiale, les contrastes sont meilleurs par diminution du diffusé en provenance du patient.
- utiliser l’algorithme de reconstruction OS EM-ML 6 itérations : il donne une meilleure résolution et un meilleur contraste que EM-ML 20 itérations. Il est par ailleurs plus rapide.
- traiter les images à l’aide du filtre de WIENER coefficient 0,1 ou 0,3 : l’utilisation de ces filtres entraîne un renforcement du contraste au moins pour les objets les plus visibles et améliore l’esthétique de l’image.
Ces données ont été utilisées dans les explorations scintigraphiques en oncologie en particulier dans la pathologie pulmonaire et pleurale publiées par l’équipe (Melloni 2001 et 2004).